게임 개발에서는 벡터 연산을 자주 사용한다. 이는 벡터로서의 접근이 직관적이며, 방정식이나 복잡한 계산을 피하고
문제를 훨씬 쉽고 간단하며 효율적으로 해결하게 해주기 때문이다. 그래서 물리 엔진을 만들 때
벡터 연산의 적용을 가장 우선적으로 염두해 두는 것이 일반적이다.
속도, 바람, 저항, 충돌, 위치 판단 등 많은 것들이 벡터로 표현된다.
벡터 연산에서 가장 기본은 바로 내적과 외적이다.
먼저, 벡터의 내적은 아래와 같이 정의한다.
A*B = |A| |B| cosθ
즉, A, B 벡터의 내적은 A 벡터와 B 벡터의 크기를 각각 곱한 다음 사이각의cosθ 값을 곱한 스칼라 값이 된다.
벡터와 벡터의 내적의 결과는 벡터가 아닌 스칼라 값이다.
1. 두 단위벡터가 평행하면 절대값 1이다.
벡터 두개가 평행하는 경우는 같은 방향으로 향하거나, 반대 방향으로 향하는 것이다.
따라서 cosθ 값이 1혹은 -1이다. 절대값이 취하면 1이 된다.
내적을 이용하는 예를 몇가지 들어보면
1) 주인공의 방향벡터가 있고, 적이 주인공의 앞에 있는지 뒤에 있는지 판별

나와 적의 거리 차이로 나오는 벡터 A와 나의 Forward 벡터 간에 내적을 하면
각도가 -90 - 90 사이에 있으면 앞에 있는 것이고, 반대는 뒤에 있는 것이다.
따라서 내적시에 cosθ 값이 0보다 크면 앞쪽에, 0보다 작으면 뒤쪽에 있는 것으로 판별이 가능하다.
내적에 대해서는 이 정도로 정리하고, 이제 외적에 대해서 알아보도록 하겠다.
벡터의 외적의 결과는 내적과 달리 또 다른 벡터이다.
외적은 행렬식으로 계산할 수 있는데, 주로 사용하는 3차원 벡터의 3*3 행렬식의 풀이는 다음과 같다.

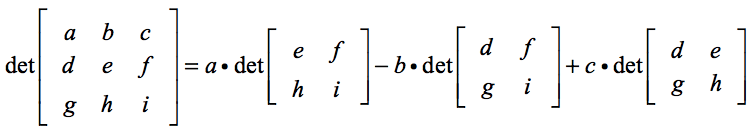
또한, AxB 외적 벡터의 방향은 수학에서는 오른손 법칙을 사용한다.
게임은 엔진이 사용하는 좌표계에 따라 다른데, OpenGL에서는 오른손 법칙, Unity는 왼손 법칙에 따르게 되어있다.
두 벡터의 외적의 결과는 역시 벡터이다. 그리고 외적 벡터의 크기는 두 벡터의 크기에 sinθ를 곱한 값과 같다.
외적의 특성은 다음 몇가지로 정리된다.
1) A와 B 벡터의 외적, AxB는 A와도 수직(perpendicular)이고, B와도 수직이다.
2) 내적과 달리 교환 법칙이 성립하지 않으며 순서를 바꾸면 반대 방향의 벡터가 나온다.
v x u = -(u x v)
3) 내적과 동일하게 분배 법칙은 성립한다.
u x (v + w) = (u x v) + (u x w)
4) 외적 벡터의 크기는 평행 사변형의 넓이이다. (밑변 * 높이로 구하는 평행 사변형 넓이에서 sinθ 값이 높이)
5) 두 벡터가 평행하면 크기는 0이다. sin0 의 값이 0이기 때문이다.
<외적을 실제 개발에서 적용하는 상황>
1) 평면의 법선 벡터를 구할 때.
삼각형의 세점을 알고 있다고 하였을 때, 벡터 2개를 구할 수 있게 되고, 그 두 벡터의 외적을 구하면 해당 삼각형이 속한 평면의 법선 벡터를 구해낼 수 있게 된다. 보통 모델링 데이터의 폴리곤 노멀 벡터를 구할 때 많이 사용한다.
2) 적이 캐릭터의 좌우 방향에 있는지 판별할 때.
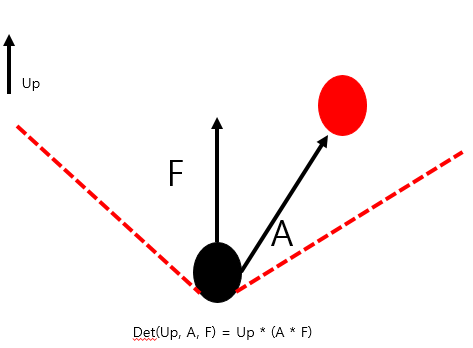
월드 좌표계의 Up 방향 벡터를 캐릭터의 Forward 방향 벡터를 F, 캐릭터와 적간에 생기는 벡터를 A 벡터라고 하면,
Up · (A × F) 값, 즉 Det(Up, A, F) 값이 0보다 크면 오른쪽, 0 보다 작으면 캐릭터의 왼쪽에 있음을 판별할 수 있다.
이는 외적으로 생긴 벡터의 방향이 Up 벡터의 방향과 -90~90도
즉, 예각을 이루면 cos값이 0보다 큰 원리를 이용한 것이다.
'Programming > Soft Renderer_2019' 카테고리의 다른 글
| #10 삼각형 내부 외부 판별 (0) | 2019.12.16 |
|---|---|
| #9 백페이스 컬링 (0) | 2019.12.16 |
| #7 내적을 사용한 시야 판별 (0) | 2019.12.16 |
| #6 평면의 방정식과 D의 의미 알아보기 (0) | 2019.12.16 |
| #5 투영 벡터 공식 유도 (0) | 2019.12.16 |