
w를 v에 투영한다는 것은
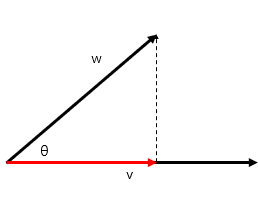
일직선의 벡터를 얻고 싶다는 것을 뜻한다.
직각 삼각형이므로 cosA = 밑변/빗변
cosA = ||v|| / ||w||
||v|| = ||w||cosA
빨간 선의 길이 = ||w||cosA
길이는 구했지만, 우리가 얻고 싶은 것은 벡터이다.
길이가 1인 v를 방향 벡터와 길이를 곱해주면 구하고자 했던 벡터를 구할 수 있다.
v의 방향 벡터 = v / ||v||
투영벡터 = ( v / ||v|| ) * ||w||cosA
하지만 두 벡터 사이의 각 A를 우리가 평소에 알리가 없다.
그래서 쓰는 차선책 v * w(v와 w의 내적) = ||v|| ||w|| cosA라는 사실을 응용하여
(v * w) / ||v|| = ||w|| cosA 이런 식을 만들어 낸다.
그래서 두 벡터만 주어졌을 때, 한 벡터를 다른 벡터에 투영하는 공식은
투영 벡터 = ( (v * w) / ||v||) * ( v / ||v|| )

가 나오게 된다.
'Programming > Soft Renderer_2019' 카테고리의 다른 글
| #7 내적을 사용한 시야 판별 (0) | 2019.12.16 |
|---|---|
| #6 평면의 방정식과 D의 의미 알아보기 (0) | 2019.12.16 |
| #4 벡터 내적 공식 유도 : a · b = |a| |b| cosθ 유도하기 (0) | 2019.12.16 |
| #3 카메라의 뷰 좌표계의 LookAt 행렬 유도하기 (0) | 2019.12.16 |
| #2 오일러각 입력에 따라 Forward, Up, Right 벡터를 구하고 이를 토대로 3차원 회전 행렬 구하기 (0) | 2019.12.16 |