앞에서 설명한 Norm이 1인 복소수

가 복소수 (cosΘ, sinΘ)와 같다고 하였을 때,
복소수 z = (cosΘ, sinΘ)의 역수는 z = (cosΘ, -sinΘ)가 나오게 된다.
여기서 z = (cosΘ, sinΘ)는 회전 행렬을 의미하고 z = (cosΘ, -sinΘ)는 회전의 역행렬을 의미한다.
(cosΘ sinΘ)를 정의해서 (x, y) (cosΘ, sinΘ)를 풀어보면
(xcosΘ - ysinΘ) + (xsinΘ + ycosΘ)i
= (xcosΘ - ysinΘ, xsinΘ + ycosΘ) 가 나오게 된다.
복소수 회전이 행렬과 동일함을 이용해, 복소수를 행렬로 표현을 하면 다음과 같다.
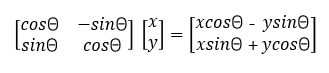
다음은 Norm이 1인 복소수 (cosα, sinα)와 (cosβ, sinβ)의 곱이 (cos(α+β), sin(α+β))와 동일함을 증명해보자
- (cosα, sinα)와 (cosβ, sinβ) 의 곱
(cosα, sinα) = α만큼 회전
(cosβ, sinβ) = β만큼 회전
a b c d
(cosα, sinα) * (cosβ, sinβ)
= ( ac - bd, ad + bc)
= (cosα cosβ) - (sinα sinβ), (cosα sinβ) + (sinα cosβ)
- (cos(α+β), sin(α+β))

- 허수부를 나타내는 행렬 및 그 특징과 의미
- cosΘ + sinΘ i(회전 행렬)을 행렬로 표현

이 행렬을 실수부와 허수부로 나누게 되면 아래와 같이 나오게 되고

나눠진 상태에서 cosΘ와 sinΘ를 앞으로 빼면 다음과 같이 나오게 된다.

a + bi => a * I(실수부) + B * J(허수부)
허수끼리 곱해주게 되면

가 나오게 되는데 이것은 허수의 정의

와 같다고 볼 수 있다.
'Programming > Soft Renderer_2020' 카테고리의 다른 글
| GameEngine 3D : Space, Rotation, Camera (0) | 2020.06.17 |
|---|---|
| 지수 함수, 맥클로린 급수 (0) | 2020.06.12 |
| 복소수의 기본 성질 (0) | 2020.06.12 |
| GameEngine 2D : Hierarchy System (0) | 2020.06.09 |
| GameEngine2D : Circle, CameraCircleBound (0) | 2020.06.02 |