Gyong

• 객체 지향 프로그래밍이란?

프로그래밍에서 필요한 데이터를 추상화시켜 상태와 행동을 가진 객체를 만들고 그 객체들 간의 상호작용을 통해

로직을 구성하는 방법.

• 객체 지향 프로그래밍의 장단점

장점

1. 코드 재사용이 용이하다.

2. 유지보수의 용이성

3. 협업을 할때 업무 분담이 쉬움

단점

1. 처리속도가 느림

2. 설계를 하는 것에 대한 많은 시간이 소요

• 객체 지향 프로그래밍 키워드 5가지

1. 클래스 : 객체를 정의하는 틀

2. 추상화 : 객체들의 공통 특징을 뽑아 하나의 클래스로 표현하는 것

3. 캡슐화 : 데이터의 구조와 데이터를 다루는 방법을 결합시켜 묶는 것

4. 상속성 : 상위 개념의 특징을 하위 개념이 물려받는 것

5. 다형성 : 다양한 형태로 표현이 가능한 구조

절두체 컬링(Frustum Culling)

- 3차원 월드에는 대단히 많은 폴리곤과 오브젝트가 있지만, 이들 중에서 실제로

 카메라의 시야범위에 포함되는 것들만 렌더링하고, 나머지 것들은 렌더링 하지 않는 기법을 말한다.
- 절두체 컬링은 3D 렌더링 기법에 있어서 가장 중요한 속도 증가 기법 중 하나이다.

절두체란?

- 투영행렬을 계산할 때 범위의 모양이 삼각뿔의 머리를 잘라놓은 것 같다고 해서 절두체라고 부른다.

- 절두체는 총 6개의 평면으로 이루어져 있다.

절두체를 이루는 6개의 평면

근평면 : 카메라와 수직하며 제일 가까운 곳의 시야 범위를 나타내는 평면

원평면 : 카메라와 수직하며 제일 먼 곳의 시야 범위를 나타내는 평면

좌평면 : 카메라의 좌측 시야 범위를 나타내는 평면

우평면 : 카메라의 우측 시야 범위를 나타내는 평면

상평면 : 카메라의 상단 시야 범위를 나타내는 평면

하평면 : 카메라의 하단 시야 범위를 나타내는 평면

6개의 평면 내부와 외부를 판단하기 위해 평면의 방정식이라는 수학적 도구를 사용한다.

프러스텀 컬링 원리

절두체 내부에 점이 포함되는지 판단하기 위해서는 6개의 평면 방정식에 점의 좌표를 대입해

모든 평면 방정식의 결과값이 양수(+)이면 절두체 내부에 포함되어 있는 것이다.

<왼손, 오른손 좌표계>

공간 좌표에서 z축을 결정하기 위한 방법이다. 

좌표계를 표현할 땐 보통 아래의 그림과 같은 왼손 좌표계와 오른손 좌표계 두 가지 방법을 이용한다.

게임 캐릭터를 씬 상에 불러와서 좌표값을 초기화 시켜보면 사용자는 캐릭터의 앞 또는 뒷모습을 보게된다.

왼손 좌표계에서는 관찰자(Player)가 오브젝트의 뒷면, 오른손 좌표계에서는 오브젝트의 정면을 본다.

유니티는 왼손 좌표계를 사용하므로 카메라에 비치는 것은 오브젝트의 뒷면,

언리얼은 유니티와 같은 왼손 좌표계를 사용하지만 방향이 다르다.

언리얼 엔진에서의 Forward Vector는 ( 1, 0, 0 ), Right Vector는 ( 0, 1, 0 )이다.

여기서 X, Y, Z축의 좌표축을 나타내는 기즈모라는 아이콘이 있는데,

이것은 공간 좌표계를 생각하면 된다.

또는 플레밍의 왼손법칙을 생각하면 쉽다.

전류 : X방향

힘이 : Y방향

자기장 : Z방향

툴에서 사용하는 좌표계는 아래와 같다.

왼손 좌표계 : DirectX, UnrealEngine, UnityEngine

오른손 좌표계 : 그래픽 라이브러리 / OpenGL, 3ds max

선 그리기를 할 때 그릴 선이 어디 위치에 있는지 구하려면 실수 연산이 필요한데

이를 정수연산으로만 끝낼 수 없을까에서 찾아본 결과 "브레젠험알고리즘"이란 것을 발견하였다.

Bresenham의 선 알고리즘 :

-> 실수 연산이 필요 없고 정수 연산만으로 처리되는 속도가 매우 빠른 래스터 방식

-> 컴퓨터 그래픽에서 선을 긋는 알고리즘.

https://translate.google.co.kr/translate?hl=ko&sl=en&u=https://en.wikipedia.org/wiki/Bresenham%2527s_line_algorithm&prev=search

실수연산이 정수연산에 비해서 매우 느린 것도 이유가 되고,

화면에 그려질 때도 정수단위의 픽셀에 그려지기 때문에 정수 연산만으로 처리하는 것이 더 좋다고 한다.

x의 변화량이 y의 변화량 보다 크다면

위와 같은 그림으로 그려지게 될 텐데 xi와 xi + 1까지는 y값이 더 가깝기 때문에 yi에 점이 그려지고

xi + 2때는 y값이 yi + 1에 더 가깝기 때문에 yi + 1에 그려져야 나름 부드럽게 보이는 선이 만들어지게 된다.

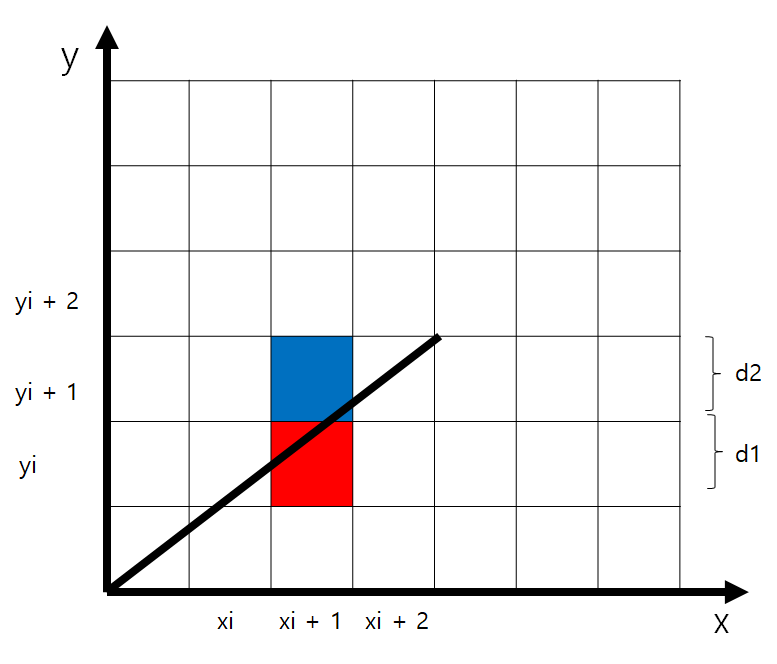
방정식에 의해 나온 y값이 정수값인 yi와 yi + 1중 어디에 가까운지 판단하는 것 부터 생각해보면 된다.

위에 그림처럼 d1과 d2값을 구해 더 차이가 적은 쪽을 선택하면 된다.

직선의 방정식 : mx + b ( m는 기울기, b는 y절편 ) m = dy / dx

d1 = m(xi + 1) + b - yi

d2 = (yi + 1) - m(xi + 1) - b

계산 한 번으로 어디에 가까운지 판단하기 위해서 위에 두 식을 합쳐야 한다.

d1 - d2를 구해 이 값이 0보다 작다면 d1이 작다는 의미로 판단할 수 있고,

0보다 크다면 d2가 더 작다는 것을 알 수 있다.

d1 - d2 = m(xi + 1) + b - yi - (( yi + 1 ) - m(xi + 1) - b )

           = m(xi + 1) + b - yi - ( yi + 1 ) + s ( xi + 1)  + b

           = 2m(xi + 1 ) + 2b - 2yi - 1

식을 x와 y값을 이용해서만 계산할 수 있게 하기위해 m = dy / dx를 넣어 정리해준다.

d1 - d2 = 2(dy / dx) (xi + 1) + 2b - 2yi - 1

해당 값의 부호만 판단하면 되기 때문에 굳이 비용이 많이 드는 나누기 연산을 할 필요가 없다.

따라서  dx를 양변에 곱해준다.

dx(d1 - d2) = 2(dy)xi + 2dy + 2b(dx) - 2(dx)yi - dx

b , dx, dy값은 변화하지 않는 상수이므로 한 번만 계산하면 된다.

위의 식을 다시 이쁘게 정리 해보면,

dx( d1 - d2 ) = 2(dy)xi - 2(dx)yi + 2dy - dx + 2b(dx)

                 = 2(dy)xi - 2(dx)yi + 2dy + dx(2b - 1)

2dy + dx(2b - 1)로 인해 dx, dy, b의 값을 알 수 있기 때문에 계산을 하고 한 변수에 넣어 두면 된다.

식에서도 보기 쉽게 2dy + dx(2b - 1)를 A로 표현하겠다.

브레젠험 알고리즘은 이전 값을 이용하여 다음 값을 찾는 형식으로 루프를 돌게 되어있다.

이전 값을 Pi라 하고 그 이후의 값을 Pi + 1이라고 하자.

Pi = 2(dy)xi - 2(dx)yi + A

Pi+1 = 2(dy)xi + 1 - 2(dx)yi + 1 + A

이전 Pi값에 계속 값을 더해주어서 다음 값을 찾는 방법을 이용하기 때문에 더해줘야 되는 값을 구하기 위해

Pi + 1에서 Pi를 빼보겠다.

Pi + 1 - Pi - 2(dy)xi+1 - 2(dx)yi + 1 + A - 2(dy)x + 2(dx)y - A

= 2(dy)(xi + 1 - xi) - 2(dx)(yi+1 - yi)

지금은 무조건 한 칸씩 옆으로 가니까 dx가 dy보다 크다고 가정을 한 상태에서 식을 세우고 있기 때문에

xi+1 - xi = 1 이 된다.

대신 y값은 이전과 같은 점일 수도 있고 한 칸 움직인 점일 수도 있다.

그렇기 때문에 위의 식에서 부터 두 가지 경우에 대한 식으로 정리할 수 있다.

1. yi+1 - yi = 0 일 때 : 2(dy) -> Pi + 1 = Pi + 2(dy)

2. yi+1 - yi = 1 일 때 : 2(dy) - 2(dx) -> Pi+1 = Pi + 2(dy) - 2(dx)

이를 통해 다음 P값을 구할 수 있는 식을 구하게 되었다. 

현재 상황의 경우에는 처음 점을 (x1, y1)으로 두고 그 다음 점을 (x1 + 1, y1 + 0.5)로 두고 구하면 된다.

x는 1씩 증가하지만 y는 어떻게 될 지 모르기 때문에 절반 값만 넣어주었다.

위의 점화식에 넣고 구해보면 최종적으로 처음 점은 P0 = 2(dy) - (dx)가 나오게 된다.