GameEngine 3D : 사원수 대수, 사원수 회전, 사원수의 활용

[사원수 대수]

 

사원수는 어떻게 구성이 돼있냐면 복소수는 거의 비슷하지만 허수가 두 종류가 더 들어간다.

 

 

그래서 i, j, k라는 허수와 실수가 있는데,

복소수는 이제 실수와 허수 Part를 나눠서 a + bi를 (a, b)라고 한다.

 

사원수는 종류가 세 가지이기 때문에 w, x, y, z라고 흔히 얘기를 하고, 

여기서 w는 실수 나머지 x, y, z를 허수부라고 할 수 있다.

 

그런데 i, j, k는 각각 직교하는 성질을 가지고 있다.

그래서 x, y, z는 어차피 직교하기 때문에 벡터로 보게 되므로

다음과 같이 퉁쳐서 표현을 한다고 한다.

 

 

여기서

 

 

는 세 가지 요소가 들어간 벡터라고 할 수 있고,

 

따라서 다음과 같이 표현을 할 수 있다.

 

 

Pure imaginary quaternion(순허수)

 

 

실수부가 0인 것.

 

Addition operator(사원수 덧셈)

 

 

실수부끼리 더하고 각각 직교하는 허수부끼리 더해서 만드는 것.

 

그리고 여기서 x, y, z ,w w ∈ F는 체에 속한다고 할 수 있다.

 

이렇게 했을 때 Addtion operator satisfies(덧셈 연산)에 대해서는

• Commutativity(교환법칙)
• Associativity(결합법칙)
• Identity(항등원) : 0
• Inverse(역원) : -q

이렇게 존재를 하게 된다.

 

다음 부분을 알기 전에 체(Field)라는 것은 사칙연산이 수행되는 수집합 또는 +과 · 이 있다.

 

덧셈에 대한 항등원 : 0

덧셈에 대한 역원 : 어떤 수를 덧셈 계산을 했을 때 항등원이 되는 것 즉, 음수가 되는 것

 

곱센에 대한 항등원 : 1

곱셈에 대한 역원 : 어떤 수가 곱셈 계산을 했을 때 1이 되는 것

 

그리고 체는 교환 법칙과, 결합 법칙, 분배 법칙 세 가지 법칙이 성립이 된다.

 

이것을 조금 더 수학적으로 보게 되면 군(Abelian group)이라고 한다.

군은 (R, +) 교환 법칙, 결합 법칙, 항등원, 역원 이런 수체계가 존재하는 것을 "군"이라고 한다.

 

실수 집합 역시 수체계가 존재하므로 군이라고 할 수 있다.

 

그리고 "군"에서 더 추가한 것을 "환(Ring)"이라고 한다.

 

여기서 추가된 것은 곱셈 연산이다.

 

군 => ( R, + )

환 => ( R, +, · )

 

환은 +, · 이 두 가지 연산에 대해서 분배 법칙이 성립하는가? 

그리고 두 번째 연산에 대해서 항등원과 역원을 가지고 있는가?

이 두 가지의 기본 조건이 존재한다.

 

그런데 여기서 한 가지 나오지 않는 것이 있다.

 

그것은 곱셈 연산에 대해서 교환 법칙이 성립하는지는 나오지 않았다.

왜냐하면 환이 되는 조건에서는 두 번째 연산자에 대해서는 교환 법칙이 필수적으로 성립이 될 필요가 없기 때문이다.

 

물론 교환 법칙이 성립이 되는 환도 존재한다.

그것은 가환환(Commutative Ring)이라고 한다.

 

그리고 여기서 교환 법칙, 분배 법칙, 항등원, 역원 이 네 가지가 성립이 되는 특수한 것이 있는데,

그것이 "체"라고 한다.

 

따라서 군, 환, 체라는 수학적 대수의 구조가 있는데,

여기서 체를 기준으로 모두가 사용을 하고 있고,

군, 환, 체로 나눈 것은 군부터 체까지 3단계로 발전된 모습이라고 이해시키기 위해서이다.

 

결론적으로 사원수의 덧셈을 다시 보게 되면 덧셈에 대해서는 항등원, 역원, 교환 법칙, 결합 법칙이 있기 때문에

군의 성질에 만족한다고 볼 수 있다.

 

Multiplication operator

 

 

여기서 실수부는 w1w2, 허수부는 x1x2, y1y2, z1z2 이렇게 되어있다.

그런데 허수부를 보면 뭔가 내적 연산과 비슷하다.

 

v1 = (x1, y1, z1), v2(x2, y2, z2)라고 했을 때

-의 내적 연산이기 때문에 -(v1 · v2)가 나오게 되고 이것은

 

 

과 같다고 볼 수 있다.

 

그런데 여기서 다음과 같이 하나만 -가 되있는 것을 볼 수 있는데,

 

 

순서가 -z1y2, -x1z2, -y1x2 이런 식으로 되어있다.

 

만약에 q2 · q1 을 하게 되면 어떻게 될까? 

결과는 다음과 같다.

 

 

Multiplication operator satisfies

 

 

그렇다면 사원수는 왜 체가 성립되지 않는가?

 

왜냐하면 곱셈은 동시성을 만족시키지 못하기 때문이다.

 

 

 

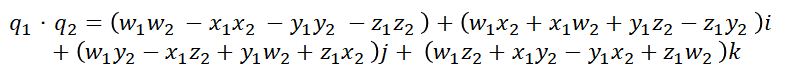
위의 식을 기반으로 사원수가 예외적으로 체의 성질을 가지는 조건은 무엇인가?

 

위의 식에서 볼 수 있듯이 서로 다른 부분이 벡터 부분이다.

그래서 다른 부분의 체가 0이 되려면 같아야 한다.

벡터 부분의 결과가 0이어야 한다는 것은

즉, 체의 성질을 가지려면 두 벡터가 평행해야 한다는 것이다.

 

 

[4차원 공간에서의 사원수 회전]

오일러 공식을 이용해 4차원 공간에서 회전을 수행하는 사원수는 어떤 형태인가?

 

 

계산을 하게 되면

 

 

이 나오게 되면서, i를 대신해서 r로 대체할 수 있게 되고, 이것은 다음과 같이 나오게 된다.

 

 

여기서 빨간 네모 부분의 형태는 4차원 공간에서의 회전이라고 할 수 있다.

 

3차원 공간 위의 벡터를 회전시키기 위해 위의 사원수를 그냥 사용하면 안 되는 이유는?

 

왜냐하면 우리는 4D 공간의 3D 부분을 사용해야 하기 때문이다.
그러기 위해서는 하나의 요소를 일정한 값으로 설정해야 한다.
그래서 사원수를 쉽게 계산을 해야하기 때문에 순허수를 사용하는 것이다.

 

 

그러나 보다시피 회전 후 실제 부분은 더 이상 0이 아니다.

즉, 4D 공간의 동일한 3D 부분에 있지 않다는 것을 의미한다.
그래서 사원수를 3D 벡터를 회전하는데 사용해서는 안 된다.

 

[3차원 공간에서의 사원수 회전]

 

쿼터니언의 핵심은 w를 0으로 만들 수 있는 방법을 찾는 것이다.

 

 

임의 축을 만들고 4차원에서의 벡터지만 3차원에서 허수부만을 가지고 있는 상태이다.

이것의 기준 벡터가 (a, b, c)라고 했을 때 이것은 r이 되고,

r의 성질은

 

 

이 된다.

 

이런 임의의 회전 축에서 3차원 공간에서 v가 있고,

v의 실수부는 0이고, 허수부는 v라고 표시를 한다.

 

그리고 v로부터 반시계 방향으로 돌리게 되면 다음과 같이 실수부가 0이고 v가 v'가 되는 형태로 나오게 된다.

 

 

그러면 이제 원점에서부터 v라는 벡터를 분해를 하는 것이다.

여기서 회전축의 수직인 부분을 v⊥라고 하고

수평인 부분을 v||라고 해보자.

 

그럼 v = v⊥ + v||이 된다.

 

이 상태에서 사원수는 분배 법칙이 적용이 되는가?

 

분배 법칙은 바꾸는 것은 되지 않지만, 순서만 맞으면 적용이 된다. 

 

그러면 이제 여기서 r을 돌렸을 때 어떻게 결과가 나오는지 생각해보자.

 

r을 기준으로 θ만큼 회전한 4차원의 형태는 (cosθ(실수부), rsinθ(허수부)) 가 나오게 된다.

그런데 다음과 같이 v||, v, v⊥는 허수부는 있지만 실수부는 없다.

 

 

 

그러면 (cosθ, rsinθ) => (0, v, v||) 이렇게 표현을 할 수 있고,

여기서 v가 q1이라고 하면 w는 0이지만

v가 q2라고 하면 w는 0이 아니게 된다.

 

이 상태에서 하나만 순허수라고 했을 때

 

 

여기서 q1이 회전이라 하고 q2가 벡터라고 가정해보면 다음과 같이 나오게 된다.

 

 

만약 둘 다 0이라면 이 상태에서 내적과 외적만 남게 된다.

 

이것은 다음과 같이 앞서서 진행했던 부분과 같은 것이고,

 

 

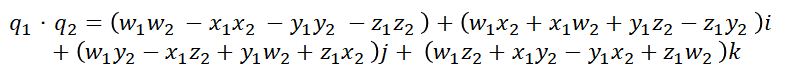
이것을 내적과 외적의 형태로 표현한 것뿐이다.

 

임의의 벡터를 두 부분으로 쪼개보았을 때 수평인 부분은

 

 

수직인 부분은

 

 

이 나오게 된다.

 

정리를 하자면

수평인 부분은 교환법칙이 성립하고,

수직인 부분은 내적이 0이기 때문에 실수부가 날라가고 허수부만 남게 된다.

 

결과적으로 수직인 부분은 교환을 하게 되면 -회전이 된다고 볼 수 있다.

 

 

지금까지 한 것을 정리해보면 다음과 같다.

 

 

내적은 영향을 받지 않는다. 하지만 외적을 하게 되면 다음과 같이 외적의 기호가 바뀌게 된다.

즉 회전축 방향이 -로 바뀐다는 뜻이다.

 

 

방정식의 첫 번째 순서가 시계 방향 회전이라면 두 번째 순서는 시계 반대 방향 회전이다.

따라서 다음과 같이 방정식을 구할 수가 있다.

 

 

이것을 증명해보면 다음과 같다.